Il fenomeno del congelamento dell’acqua con temperature positive. Come si verifica?
Congelamento dell’acqua con temperature positive, come è possibile?
ROMA, 11 Aprile 2018 – Ci sono alcuni fenomeni che vanno contro il senso comune, alcuni più facili da osservare di altri, quali la neve con temperature positive, anche con 3-4 gradi centigradi. Meno frequente è invece il congelamento dell’acqua con temperature positive sotto irruzioni fredde. L’esempio più eclatante che ricordo era alla fine di dicembre 2014, con una temperatura di 2 gradi attorno a mezzogiorno, l’acqua ghiacciava sotto i colpi della tramontana. Inizialmente possiamo stupirci, in quanto la termodinamica ci dice che due corpi a contatto tendono all’equilibrio termico. Una seconda considerazione che può venire in mente di fare è che il vento sottrae più calore all’acqua. Di irruzioni fredde ne vediamo varie nel tempo, più o meno intense, ma il fenomeno non avviene sempre o non sempre è così evidente. Useremo questo caso molto didattico per capire il fenomeno ed estenderlo poi al caso della neve con temperature positive.
Congelamento dell’acqua con temperature positive
Immaginiamo dunque che sia in corso una irruzione fredda, e abbiamo la nostra vaschetta di acqua esposta al vento freddo di tramontana, e vediamo che questa congela nonostante la temperatura sopra lo 0°C.
Vediamo quello che succede: l’acqua della vasca tenderà ad evaporare. L’evaporazione dell’acqua avviene se l’acqua non è troppo fredda, ma un altro modo di far evaporare l’acqua è quello di rendere l’ambiente circostante secco: se immaginiamo la nostra vasca al chiuso con aria secca, l’acqua evapora fino a che non si arriverà ad un equilibrio per cui tante molecole di vapore escono dall’acqua, e altrettante condensano e ritornano ad essa. Ossia l’ambiente è saturo. Se esponiamo la vasca a un flusso di aria secca, la vasca evapora, ma non trova mai un equilibrio, perché l’ambiente è sempre soggetto a un ricambio di aria di nuovo secca.
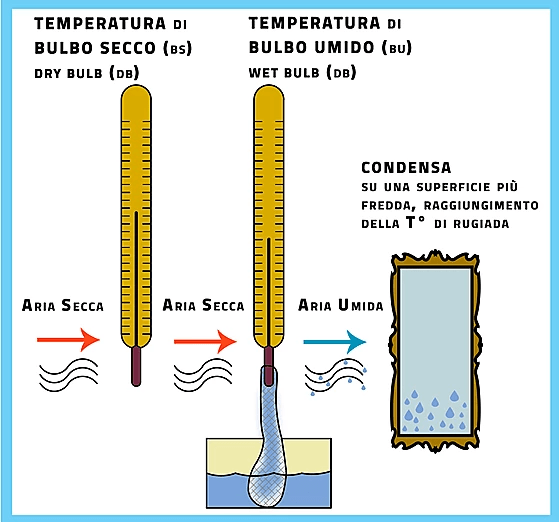
A questo punto potreste essere confusi, in quanto l’evaporazione dell’acqua avviene se la riscaldo, mentre qui si è descritto un processo osmotico. L’evaporazione, per avvenire, ha effettivamente bisogno di calore e lo sottrae all’acqua della vasca, la cui temperatura di conseguenza scende. Questo vuol dire che, pure se ho una temperatura di 2 gradi ma aria secca e ben ventilata, l’acqua della mia vasca evapora fino al congelamento. La temperatura dell’acqua può scendere a temperature anche di svariati gradi in meno dell’aria. Quindi sotto irruzione continentale come quella descritta a inizio articolo, con una temperatura di 2 gradi il congelamento è stato possibile perché l’evaporazione forzata dell’acqua, a causa del flusso di aria secca, ha sottratto a questa il calore facendola scendere sotto lo zero, anche di qualche grado.
Il fenomeno è ben noto, e la temperatura raggiunta dall’acqua è chiamata temperatura di bulbo umido, e come dimostra l’esempio è un parametro importante nelle previsioni meteorologiche.
È più facile notare che il ghiaccio che si forma sotto irruzione è più spesso, anche molto più spesso di quello che si forma in una nottata serena invernale senza vento, con raffreddamento notturno da inversione termica. In caso di nottata fredda invernale con calma di vento, se l’aria è a 0 gradi non è neanche detto che vi sia congelamento (gli 0 gradi rappresentano una transizione di fase in cui solido e liquido ancora convivono in equilibrio, questo è il caso in cui l’acqua si porta alla stessa temperatura dell’aria). Se è in corso una irruzione continentale con la stessa temperatura (magari è la massima del giorno) vedrete formarsi belle lastre!
Neve con temperature positive
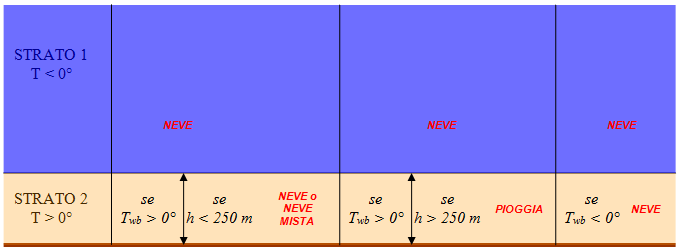
Veniamo al caso più interessante: neve con temperature positive. In questo caso, la goccia di pioggia che scende sente un flusso addosso, che in caso di aria secca (dunque non necessariamente ventilato, dal sistema di riferimento della goccia è l’aria circostante a muoversi, non la goccia!) ne provoca l’evaporazione. Vale sempre che la temperatura delle gocce quando arrivano al suolo, è la temperatura di bulbo umido. Dunque anche in questo caso se la colonna d’aria è piuttosto secca, la goccia può diventare fiocco e conservarsi anche con temperature più che positive. Attenzione però, se vedete nevicare con 1-2 gradi, nulla di strano, la temperatura di bulbo umido non c’entra niente, semplicemente il fiocco incontra strati con temperature positive senza che faccia in tempo a sciogliersi prima di atterrare. Se il fenomeno avviene con aria secca e temperature sopra i 2 gradi, allora la temperatura di bulbo umido ci da una spiegazione. Può capitare di vedere fioccate con 3-4 gradi. Il mantenimento del fiocco è possibile grazie all’aria secca.
A questa categoria potrebbe appartenere la nevicata di roma del gennaio 2016. Nevicata anche in centro, con temperature ampiamente positive. Ecco un video girato durante quell’evento nevoso:
https://www.facebook.com/CEMER.it/videos/1156508371033707/
Nel caso non trovaste in rete questo parametro nelle carte dei modelli,la temperatura di bulbo umido la si può calcolare in questo modo: nella descrizione fisica del fenomeno, si impone che l’entalpia dell’ambiente e dell’acqua siano la stessa. Quindi ne ricaviamo la seguente equazione:
\(\displaystyle{T_{\mathrm{wb}}+\frac{\lambda}{c_p}r_{\mathrm{sat}}=T+\frac{\lambda}{c_p}r}\)dove \(T_{\mathrm{wb}}\) è la temperatura di bulbo umido, \(\lambda\) è il calore latente del passaggio di fase, \(c_p\) è il calore specifico dell’acqua a pressione costante, \(r\) è la massima quantità di vapore che l’aria può contenere a quella temperatura e pressione senza sovrasaturare (di solito si trova l’UR in rete, ma qui \(r\) è la stessa quantità espressa non in percentuale, ma in valore assoluto grammi/chili).
A secondo membro abbiamo \(T\) come temperatura dell’aria, \(\lambda\) calore latente di questa (anche questo parametro non lo si trova sul web, ma lo si può ricavare come differenza della temperatura potenziale equivalente con quella potenziale (entrambe ad una data quota) moltiplicata per il calore specifico dell’aria in quelle condizioni atmosferiche, \(c_p\) si ripete a denominatore e \(r\) è il mixing ratio dell’aria, sempre espresso in valore assoluto e non in UR.
Riscriviamo l’uguaglianza come:
\(\displaystyle{T_{\mathrm{wb}}+\frac{\lambda}{c_p}r_{\mathrm{sat}}=T+(θ_e-θ)r}\)
Tutti i dati della formula sopra si trovano facilmente in rete,basta isolare al primo membro \(T_{\mathrm{wb}}\) e il gioco è fatto.
Di Claudio Giulianelli