Coronavirus: R0 e l’ultima nostra ANALISI dei dati nazionali
24/04/2020 – le ultime analisi sui dati ufficiali dell’epidemia da coronavirus covid-19 in Italia, con estensione dello studio al parametro R0 e alla positività.
Torniamo a parlare di coronavirus facendo il punto della situazione in Italia, basandoci sull’analisi da me condotta dei dati ufficiali aggiornati ad oggi 24 aprile 2020. Nei precedenti due editoriali ho deciso di utilizzare un nuovo modello, il PL-ECO, per simulare l’andamento dei decessi e dei nuovi casi giornalieri, che si è rivelato essere finora decisamente stabile e attendibile.
Nello studio di oggi ho incluso due ulteriori parametri rispetto a quelli precedenti, che sono l’indice R0 e la positività.
R0 è il numero di riproduzione di base cioè, in parole povere, il numero di persone che una persona positiva al virus infetta, in media. Questo indice ci dà perciò indicazioni sulla contagiosità di un morbo. Applicando opportune restrizioni, si può ridurre progressivamente l’R0 e rendere la malattia meno trasmissibile. Se si arriva a un valore inferiore a 1, significa che mediamente una persona positiva non riesce a trasmettere il virus a neanche una persona. Per definizione (vedi note in fondo), quando R0 diviene uguale a 1 l’epidemia finisce: infatti il numero di casi totali va ad eguagliare la somma dei guariti con i decessi, detta anche casi rimossi.
Non vogliamo qui entrare nel merito di una descrizione rigorosa e delle difficoltà che ci sono nel suo calcolo e nelle interpretazioni. Ci limitiamo solamente a precisare che R0 indica il numero di riproduzione medio dell’epidemia: in altre parole, la stima di R0 relativa al giorno X tiene conto di tutto quello che è successo dal primo giorno fino al giorno X. Questa precisazione è doverosa, perché ci si potrebbe confondere con il tasso di riproduzione istantaneo, spesso indicato con R(t), che invece tiene conto solamente di quello che è successo tra il giorno X e quello precedente, e che in questi giorni è stimato inferiore a 1.
La positività è la percentuale di persone che risultano positive al covid-19 tra quelle sottoposte all’analisi (tampone). È interessante studiare la positività perché ci dà una informazione sui contagi tenendo conto del numero di tamponi effettuati: se il suo valore diminuisce, significa che a parità di tamponi ci sono meno persone positive in più, e possiamo presumere che la diffusione del virus sia in calo.
LE STIME DI OGGI 24 APRILE
Vediamo ora un riassunto dei risultati ottenuti con la simulazione di oggi.
Giorno del picco dei decessi stimato: tra 29 e 31 marzo.
Numero finale di decessi stimato: 29750 ± 2167.
Giorno con 5 decessi giornaliero stimato: tra 6 e 12 giugno (tra 46 ± 3 giorni).
R0 di oggi stimato: 2.2 ± 0.1
R(t) di oggi stimato: 0.90 ± 0.04
Primo giorno con R0 minore di 1 stimato: tra 22 maggio e 15 giugno (tra 40 ± 12 giorni).
Il picco dei decessi è ormai superato da circa 3 settimane. Il fatto che R(t) sia inferiore a 1 sta a indicare che tra ieri e oggi mediamente una persona positiva è riuscita a infettare meno di una persona: ciò indica chiaramente che ci dirigiamo verso la fine dell’epidemia. Una stima di quando ciò accadrà l’abbiamo provata a dare nell’analisi che segue.
LA SIMULAZIONE IN DETTAGLIO
Riportiamo ora in dettaglio l’analisi svolta sui dati di decessi giornalieri per COVID-19 in Italia, aggiornati ad oggi 24 aprile 2020. Come sempre, l’analisi si concentra sul dato dei decessi, che è più oggettivo degli altri, sebbene questa volta viene estesa anche a R0 e alla positività.
DECESSI GIORNALIERI
Oggi si registrano 420 nuovi decessi. Ecco il grafico dei decessi giornalieri con sovrapposti dati e simulazione PL-ECO.
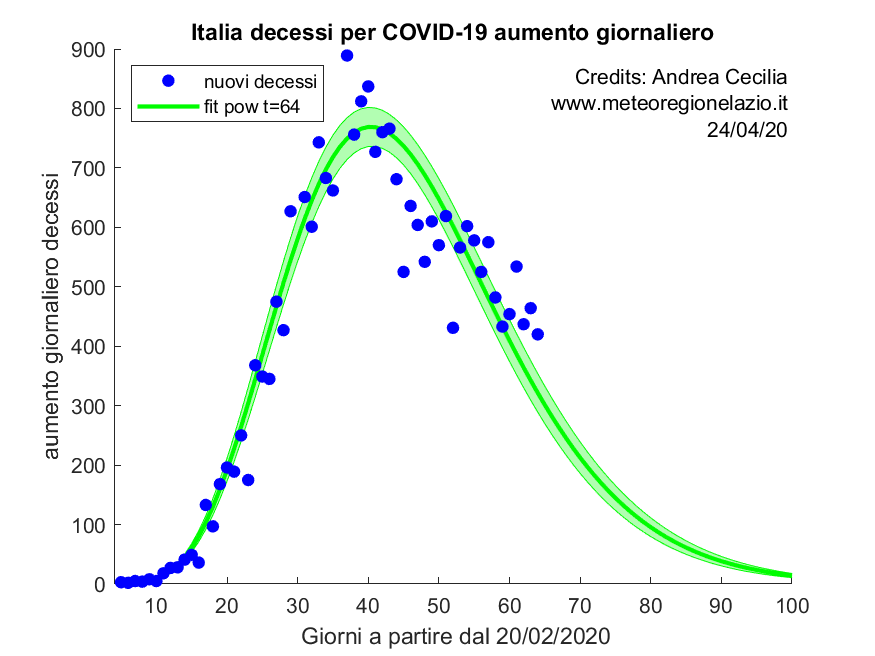
La banda verde indica l’intervallo di confidenza della simulazione fatta con modello PL-ECO, mentre i puntini blu sono i dati registrati.
Si nota come tra il 45-esimo e il 55-esimo giorno si sia misurata una certa fase stazionaria dei decessi giornalieri. Questo è dovuto all’effetto combinato della discesa dei nuovi decessi in Lombardia più lenta dell’aumento nel resto d’Italia in tale periodo.
DECESSI TOTALI
Di seguito il grafico con l’andamento dei decessi totali (valore cumulato) e la simulazione.
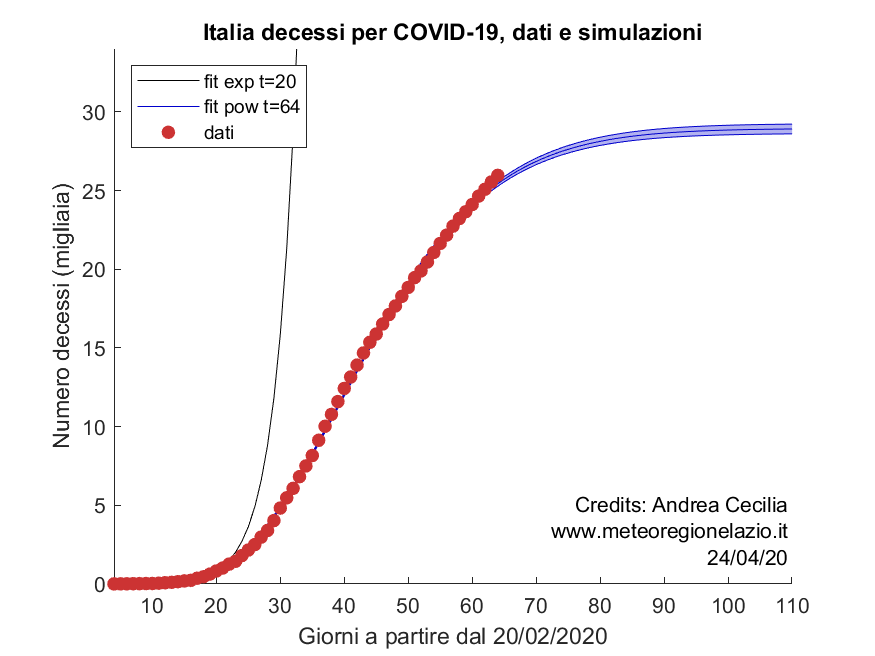
La curva nera rappresenta l’andamento esponenziale (exp) che inizialmente caratterizzava il fenomeno, che è stato abbandonato con il lockdown; quella blu è la simulazione del modello PL-ECO a legge di potenza con cut-off esponenziale (pow), più realistico.
POSITIVITÀ
Di seguito il grafico con l’andamento della positività e la simulazione.
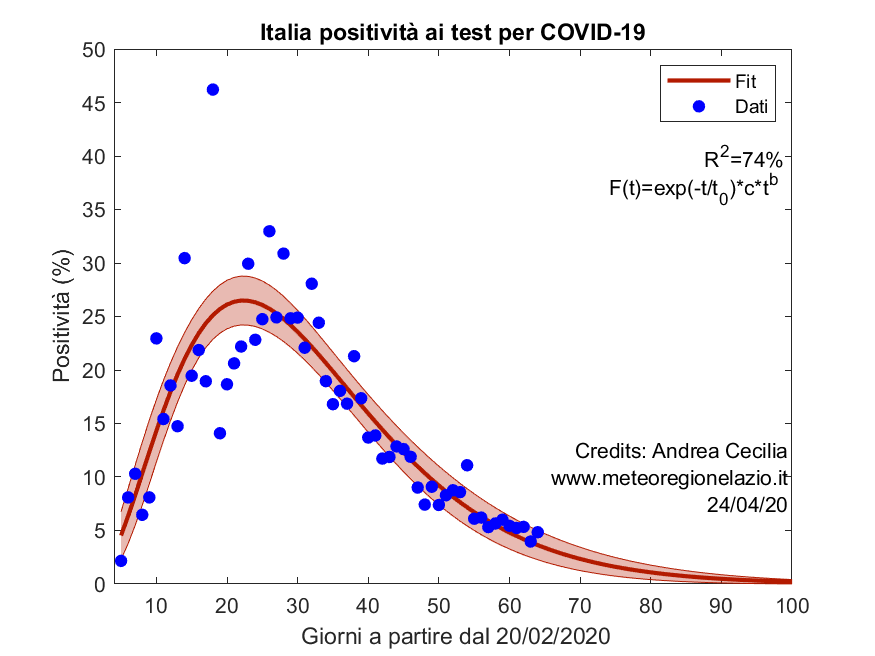
La banda rossa indica l’intervallo di confidenza della simulazione fatta con modello PL-ECO a 3 parametri, mentre i puntini blu sono i dati registrati.
Notiamo che dopo un picco di positività con valori tra 25 e 35% di oltre un mese fa, vi è stata una discesa sempre più regolare, fino al valore di oggi del 5% circa. Come dicevamo all’inizio, il fatto che la positività sia in costante diminuzione è un altro indicatore della decrescente diffusione del virus.
NUMERO DI RIPRODUZIONE R0
Di seguito il grafico con l’andamento del numero di riproduzione R0 e la simulazione.
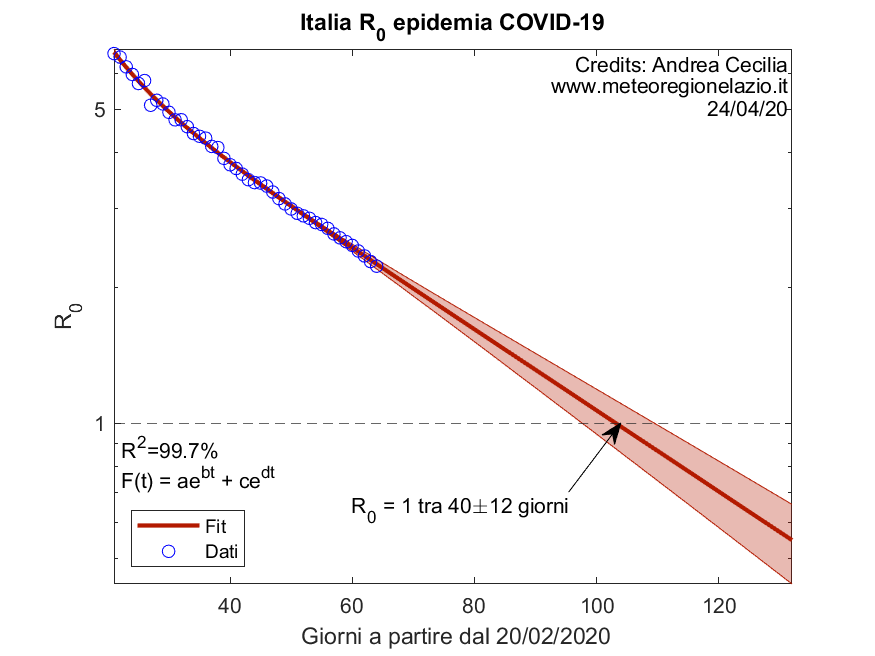
La banda rossa indica l’intervallo di confidenza della simulazione esponenziale decrescente, mentre i cerchi blu sono i dati registrati.
I valori sull’asse verticale sono riportati in scala logaritmica. Il fatto che l’andamento di R0 appaia come molto simile a una retta su questa scala ci indica che il calo è con ottima approssimazione esponenziale nel tempo: il valore del R quadro pari al 99.7% (cioè 0.997) molto vicino al 100% per questa simulazione ne è una riprova.
Come si vede, il valore del numero di riproduzione R0 viene stimato raggiungere 1 tra 40 giorni, con un errore di 12 (cioè del 30%).
ATTENDIBILITÀ
La simulazione si sta mostrando piuttosto stabile e affidabile. Di seguito la simulazione per i decessi giornalieri fatta un mese fa.
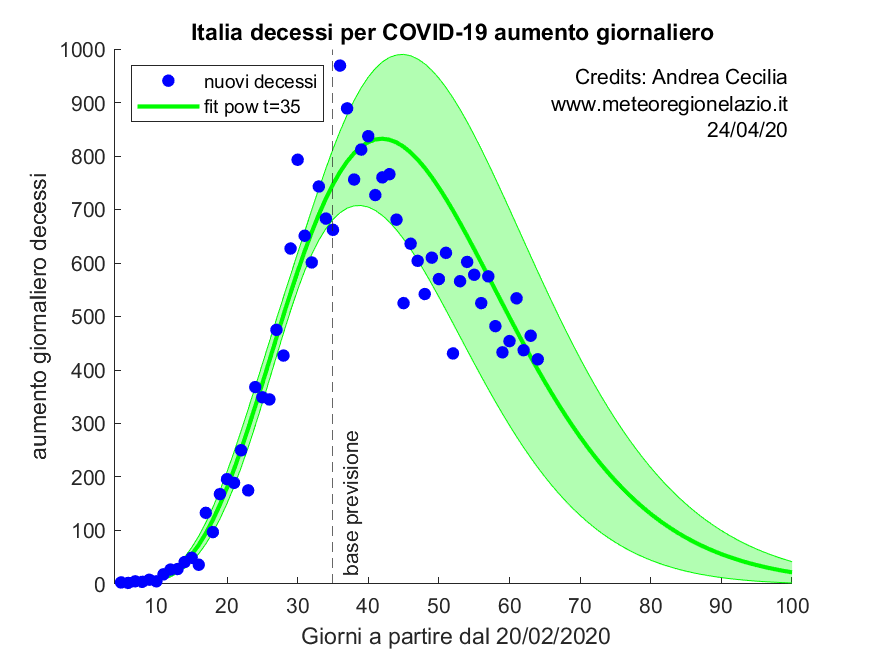
Già un mese fa il modello PL-ECO riusciva a fornire un intervallo di confidenza per l’andamento futuro decisamente realistico, visto che i dati osservati nel successivo mese ricadono perfettamente in esso.
A riprova della stabilità del modello, riportiamo l’andamento del numero finale di decessi stimato giorno per giorno.
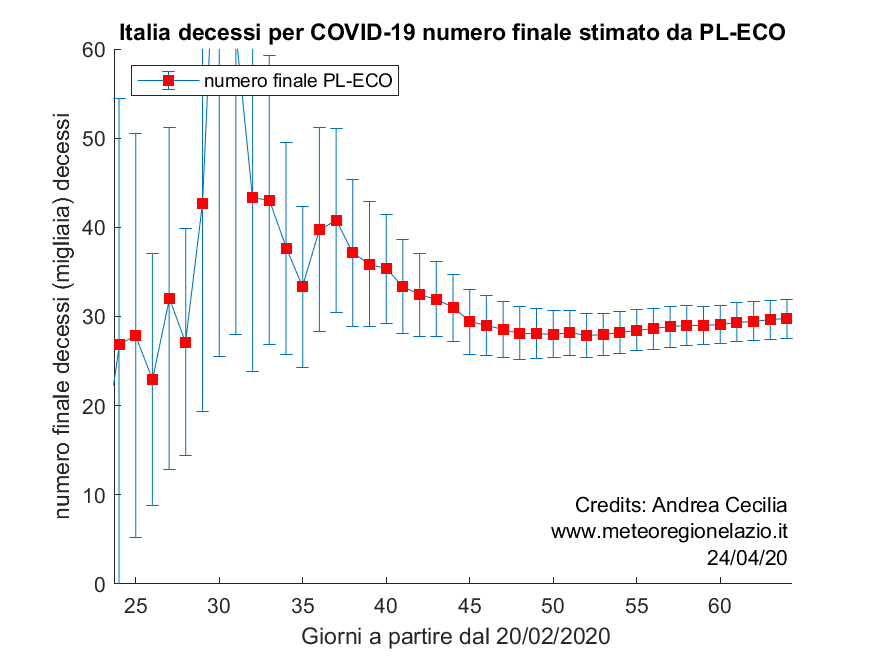
Si vede come questa stima sia molto stabile nell’ultimo mese.
È infine interessante osservare l’andamento del R quadro relativo alla simulazione PL-ECO e logistica sul numero cumulato di decessi.
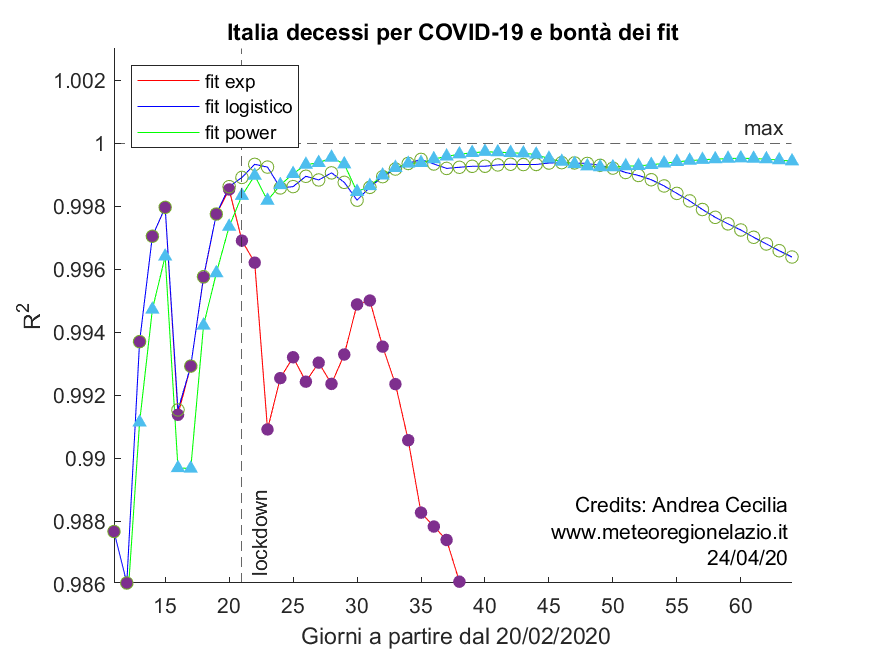
Nel grafico sono riportati i valori di R quadro per i tre tipi di simulazione esponenziale, logistica e PL-ECO (power law con cut-off esponenziale). Da una decina di giorni il modello logistico, che inizialmente era il più gettonato per fare simulazioni, stia perdendo sempre più colpi in favore del nuovo modello che rimane invece stabile.
CONCLUSIONI
Le analisi mostrano che ci siamo lasciati alle spalle il picco dei decessi da tre settimane, e siamo nel pieno della fase decrescente di contagi e decessi. Tuttavia non siamo ancora al termine dell’epidemia. Le analisi di decessi, positività e R0 sono tutte concordi nel porre almeno a fine maggio, cioè tra oltre un mese, l’ingresso nella coda finale dell’epidemia, cioè con decessi e positivi giornalieri che si possono contare sulle proprie mani.
Il numero finale di decessi stimato è stabile da quasi un mese e si attesta sui 30 mila con un errore di 2 mila.
Perciò dobbiamo pazientare ancora un po’ ed è fondamentale continuare a seguire i provvedimenti di contenimento che sono stati messi in atto.
Come sempre, ci teniamo infine a precisare che queste simulazioni si basano sull’ipotesi fondamentale di condizioni che rimangono invariate, cioè che non esplodono nuovi grossi focolai come quello lombardo, evento questo che non sta accadendo grazie alle restrizioni messe in atto.
NOTE PER GLI ADDETTI AI LAVORI
1. STIMA DI R0
Il valore di R0 è stato stimato con la formula
\[ R_0=-N\frac{\ln\left(1-\frac{T_c}{N}\right)}{M+G}\approx\frac{T_c}{M+G}\]
dove \(N \) è la popolazione suscettibile, ovvero quella italiana pari a \( N=60.36 \cdot 10^6\); \( T_c\) il totale dei casi, \(M\) e \(G\) rispettivamente il totale dei morti e dei guariti. L’approssimazione è valida in virtù del fatto che \( T_c\ll N\).
La funzione che si è utilizzato per la simulazione previsionale è un semplice esponenziale a due parametri
\[ R_0(t)=a\exp(bt)+c\exp(dt).\]
2. STIMA DELLA POSITIVITÀ
La positività è definita come
\[P(t)=100\frac{\Delta T_c (t)}{\Delta T_a (t)}\]
dove \( \Delta T_c\) è il numero di nuovi casi giornaliero e \( \Delta T_a\) quello delle analisi (tamponi) effettuate al tempo \( t\).
La funzione utilizzata nella simulazione è una power law con cut-off esponenziale (PL-ECO) a 3 parametri
\[P(t)=ct^b\exp(-t/t_0).\]
La scelta di questa funzione risiede nel fatto che la PL-ECO a due parametri
\[\left(\frac{t}{t_0}\right)^b \exp(-t/t_0)\]
ben approssima l’andamento dei nuovi casi giornalieri, che si trovano al numeratore; al denominatore invece ci sono i tamponi giornalieri, che in prima approssimazione hanno finora avuto un andamento rettilineo nel tempo.
Un doveroso ringraziamento agli utenti del gruppo Facebook Fisici e matematici contro il Covid19 per il loro grande contributo alla buona informazione, i cui lavori sono stati fonte di ispirazione per l’analisi qui presentata.
Al prossimo aggiornamento!
#iorestoacasa